library(tidyverse)
library(AMCP)
library(dfmtbx)Two-way Repeated Measures ANOVA
Building off of the one-way repeated measures ANOVA, in this tutorial I cover how to analyze data from experimental designs in which there are two repeated measures factors.
Dataset description
We will use the data from Chapter 12 Table 1 in the AMCP package. In this hypothetical study, 10 subjects are participating in an experiment that tests how visual information can interfere with recognizing letters. Each subject performs a letter recognition task in two conditions, noise absent or present. Noise refers to visual information that is presented along with either a letter T or I that the subject needs to identify. Within each condition, visual information was either presented at 0° (directly in front of the participant), at 4° (slightly offset to one side), or at 8° (even more offset to the side). Thus, noise and angle represent our within subjects factors. Finally, the dependent variable in this study is the latency in milliseconds needed to identify the letter.
# Load the data
data(chapter_12_table_1)
# Set to objected named data
data <- chapter_12_table_1
# Display as gt table
data %>%
format_gt_tbl()| Absent0 | Absent4 | Absent8 | Present0 | Present4 | Present8 |
|---|---|---|---|---|---|
| 420 | 420 | 480 | 480 | 600 | 780 |
| 420 | 480 | 480 | 360 | 480 | 600 |
| 480 | 480 | 540 | 660 | 780 | 780 |
| 420 | 540 | 540 | 480 | 780 | 900 |
| 540 | 660 | 540 | 480 | 660 | 720 |
| 360 | 420 | 360 | 360 | 480 | 540 |
| 480 | 480 | 600 | 540 | 720 | 840 |
| 480 | 600 | 660 | 540 | 720 | 900 |
| 540 | 600 | 540 | 480 | 720 | 780 |
| 480 | 420 | 540 | 540 | 660 | 780 |
Prepare the data (wide to long)
The data set from the package is in a wide format. Re-arranging the data set so that it is in long format will facilitate model fitting, summarizing data, and generating figures.
rm_data <- data %>%
mutate(id = as.character(seq(1:dim(data)[1]))) %>%
group_by(id) %>%
pivot_longer(cols = -id, values_to = "latency", names_to = "condition.angle") %>%
ungroup() %>%
separate(col = condition.angle,
into = c("condition", "angle"),
sep = -1) %>%
mutate(across(condition:angle, ~ factor(.x)))Here’s a view of the first several rows of the long format data. In this format, each subject should have 6 rows of data, one for each combination of condition and angle.
| id | condition | angle | latency |
|---|---|---|---|
| 1 | Absent | 0 | 420 |
| 1 | Absent | 4 | 420 |
| 1 | Absent | 8 | 480 |
| 1 | Present | 0 | 480 |
| 1 | Present | 4 | 600 |
| 1 | Present | 8 | 780 |
Generate summary statistics
Next we generate summary statistics to inspect the data focusing on marginal (averaged over one factor) and cell means (averaged over combinations of the factors).
Summary for angle
Once the data is in long format, we can group it by angle and summarize it using a custom function I wrote using the dplyr package.
rm_data %>%
group_by(angle) %>%
summarize_variable(latency) %>%
format_gt_tbl()| angle | n | min | max | median | mean | sd | se |
|---|---|---|---|---|---|---|---|
| 0 | 20 | 360 | 660 | 480 | 477 | 74.06 | 16.56 |
| 4 | 20 | 420 | 780 | 600 | 585 | 122.92 | 27.49 |
| 8 | 20 | 360 | 900 | 600 | 645 | 154.36 | 34.52 |
Summary for condition
Similarly, we can group the data by the noise condition and calculate the marginal means.
rm_data %>%
group_by(condition) %>%
summarize_variable(latency) %>%
format_gt_tbl()| condition | n | min | max | median | mean | sd | se |
|---|---|---|---|---|---|---|---|
| Absent | 30 | 360 | 660 | 480 | 500 | 77.73 | 14.19 |
| Present | 30 | 360 | 900 | 660 | 638 | 152.35 | 27.81 |
Summary for combinations of condition and angle
Finally, we can group by condition and angle to calculate cell means.
summary_data <- rm_data %>%
group_by(condition, angle) %>%
summarize_variable(latency)
summary_data %>%
format_gt_tbl()| condition | angle | n | min | max | median | mean | sd | se |
|---|---|---|---|---|---|---|---|---|
| Absent | 0 | 10 | 360 | 540 | 480 | 462 | 56.92 | 18.00 |
| Absent | 4 | 10 | 420 | 660 | 480 | 510 | 86.02 | 27.20 |
| Absent | 8 | 10 | 360 | 660 | 540 | 528 | 78.99 | 24.98 |
| Present | 0 | 10 | 360 | 660 | 480 | 492 | 88.54 | 28.00 |
| Present | 4 | 10 | 480 | 780 | 690 | 660 | 109.54 | 34.64 |
| Present | 8 | 10 | 540 | 900 | 780 | 762 | 116.79 | 36.93 |
Plot the data
Next, we can plot the data to reveal any patterns or trends and to visualize the distribution of the dependent variables.
Box plots
One option to visualize the data is through box plots for each angle where each condition is displayed in a separate panel. In this figure, means are indicated by a diamond.
rm_data %>%
ggplot(aes(x = angle, y = latency, color = angle, fill = angle)) +
geom_boxplot(alpha = 0.1) +
stat_summary(fun = mean, geom = "point", shape = 5, size = 3, stroke = 1) +
scale_color_manual(values = c("#440154FF","#1565c0", "#FF9993")) +
scale_fill_manual(values = c("#440154FF","#1565c0", "#FF9993")) +
facet_wrap(~ condition) +
labs(y = "Latency (ms)", x = "Angle") +
theme_minimal() +
theme(legend.position = "none")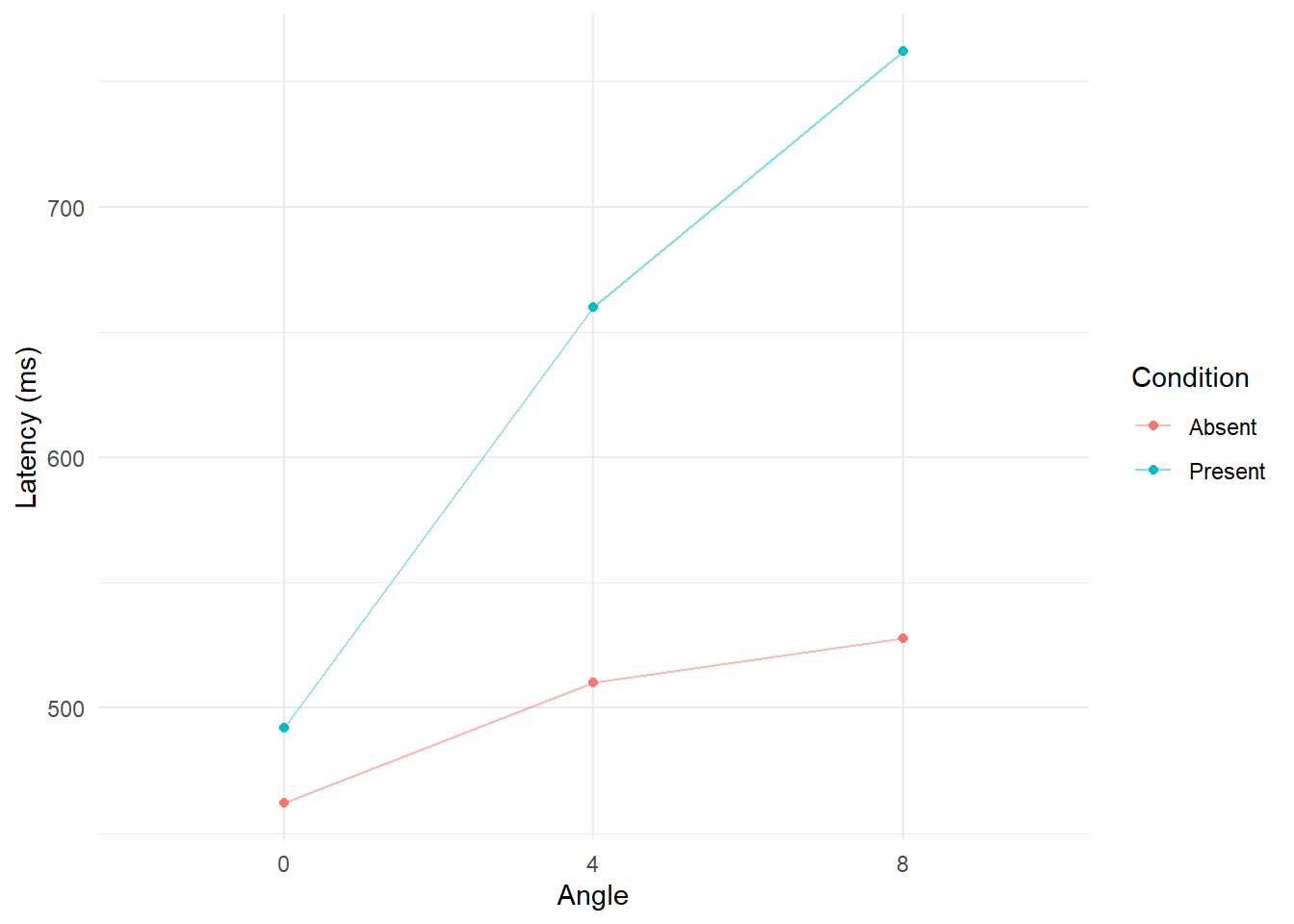
Line plots
We could also focus on the cell means and plot them in a line plot.
summary_data %>%
ggplot(aes(x = angle, y = mean, group = condition, color = condition)) +
geom_line(alpha = 0.5) +
geom_point() +
labs(y = "Latency (ms)", x = "Angle", color = "Condition") +
theme_minimal()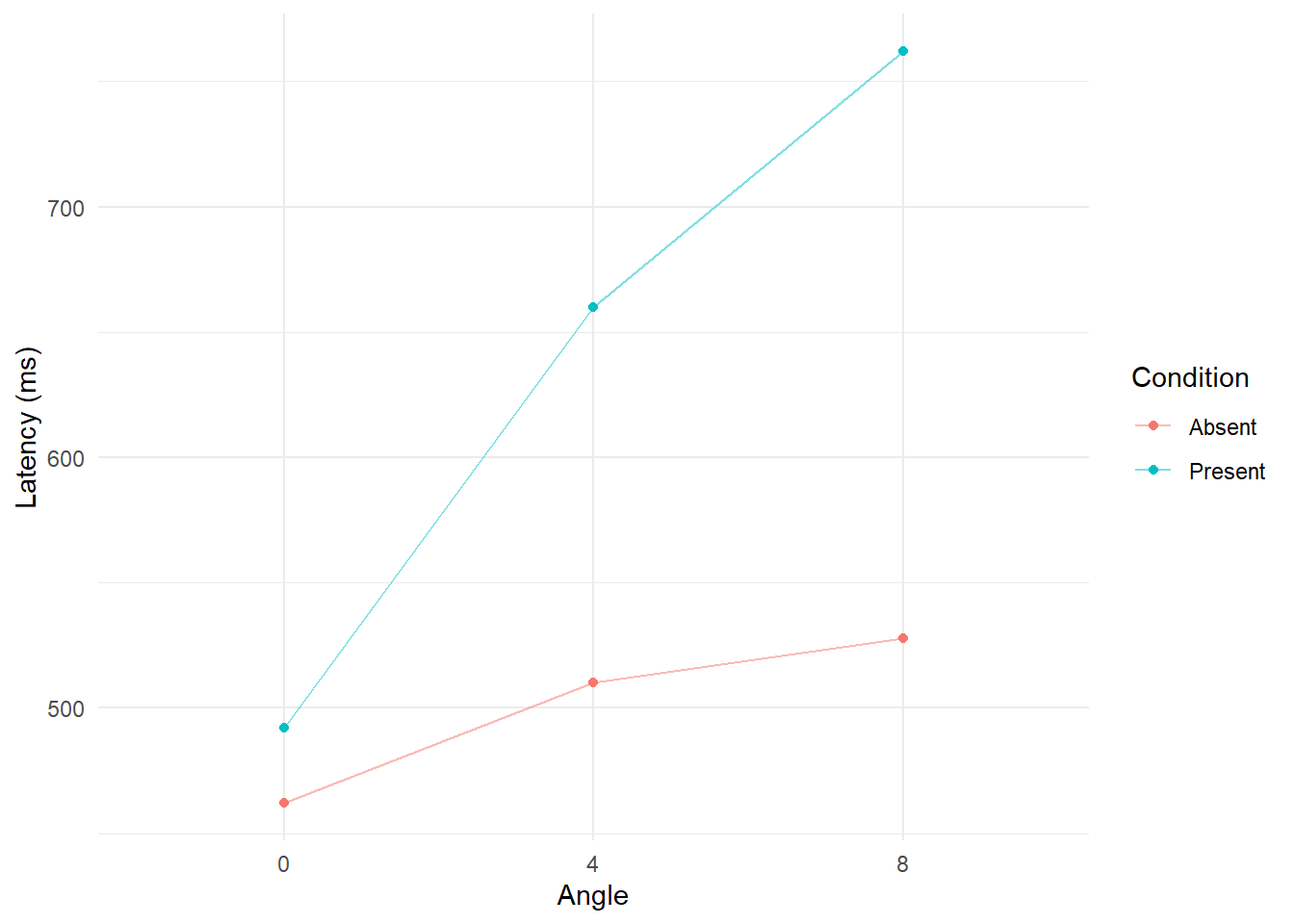
Perform two-way repeated measures ANOVA (univariate approach)
In this approach the model can be fit using the base R aov() function.
model <- aov(latency ~ angle * condition + Error(id/(angle*condition)), data = rm_data)summary(model)For this design, the output of summary(model) is a list with 4 elements. The first element contains output for the residuals of the error term for id. Elements 2, 3, and 4 contain output for the main effects for condition, angle, and the interaction between condition and angle respectively. Since elements 2 through 4 contain the main effects, I created a helper function that takes in as input a vector of the elements we want to display.
c(2, 3, 4) %>%
purrr::map_df(
.,
~ summary(model)[[.x]][[1]] %>%
as.data.frame() %>%
mutate(Source = rownames(.)) %>%
select(Source, everything())
) %>%
format_gt_tbl()| Source | Df | Sum Sq | Mean Sq | F value | Pr(>F) |
|---|---|---|---|---|---|
| angle | 2 | 289920 | 144960 | 40.72 | < 0.001 |
| Residuals | 18 | 64080 | 3560 | ||
| condition | 1 | 285660 | 285660 | 33.77 | < 0.001 |
| Residuals | 9 | 76140 | 8460 | ||
| angle:condition | 2 | 105120 | 52560 | 45.31 | < 0.001 |
| Residuals | 18 | 20880 | 1160 |
Interpretation of main effects
A two-way repeated measures ANOVA revealed a significant effect of angle F(2, 18) = 40.72, p < 0.001 suggesting that the marginal means of each level of angle are not equal to one another. In addition, the analysis revealed a significant effect of condition F(1, 9) = 33.77, p < 0.001 suggesting that mean latency scores were overall higher in the present condition compared to absent. Finally, a significant angle by condition interaction was observed F(2, 18) = 45.31, p < 0.001 indicating the the effect of condition is not the same at each level of angle.
In order to shed light on the interaction simple-effects analyses were conducted.
Effect of angle within each level condition
In the case of angle within each level of condition, we can conduct two separate one-way repeated measures ANOVAs, one for a subset of data from the absent condition and another for a subset of data from the present condition. To control for family wise error rate, a Bonferroni (.05/2, or 0.025) adjustment was implemented. These results reveal a significant simple effect of angle within the absent condition F(2,18) = 5.05, p = 0.018 and angle within the present condition F(2, 18) = 77.02, p < 0.001.
c("Absent", "Present") %>%
purrr::map_df(
.,
~ summary(aov(latency ~ angle + Error(id/angle),
data = (rm_data %>% filter(condition == .x))))[[2]][[1]] %>%
as.data.frame() %>%
drop_na()
) %>%
mutate(Source = c("Angle w/in Absent", "Angle w/in Present")) %>%
select(Source, everything()) %>%
format_gt_tbl()| Source | Df | Sum Sq | Mean Sq | F value | Pr(>F) |
|---|---|---|---|---|---|
| Angle w/in Absent | 2 | 23280 | 11640 | 5.05 | 0.018 |
| Angle w/in Present | 2 | 371760 | 185880 | 77.02 | < 0.001 |
Pairwise comparisons
Next, we follow up the significant simple-effects with pairwise comparisons of each level of angle within each condition. To control for the family wise error rate, we can use a Bonferroni adjustment where the p-value threshold determined by .025/3 (0.0083).
em <- emmeans::emmeans(model, ~ angle | condition)
emmeans::contrast(em, method = "pairwise", adjust = "none") %>%
as.data.frame() %>%
format_gt_tbl()| contrast | condition | estimate | SE | df | t.ratio | p.value |
|---|---|---|---|---|---|---|
| angle0 - angle4 | Absent | -48 | 21.73 | 28.60 | −2.21 | 0.035 |
| angle0 - angle8 | Absent | -66 | 21.73 | 28.60 | −3.04 | 0.005 |
| angle4 - angle8 | Absent | -18 | 21.73 | 28.60 | −0.83 | 0.414 |
| angle0 - angle4 | Present | -168 | 21.73 | 28.60 | −7.73 | < 0.001 |
| angle0 - angle8 | Present | -270 | 21.73 | 28.60 | −12.43 | < 0.001 |
| angle4 - angle8 | Present | -102 | 21.73 | 28.60 | −4.69 | < 0.001 |
The results indicate that at the level of condition absent, there is one significant difference after Bonferroni adjustment suggesting that mean latencies are higher at angle 8 compared to angle 0 t(28.6) = 3.04, p = 0.005. At the level of condition present, all pairwise comparisons are significantly different such that angle 0 is 168 units lower than angle 3 t(28.6) = -7.73, p < 0.001, angle 0 is 270 units lower than angle 8 t(28.6) = -12.43, p < 0.001, and angle 4 is 102 units lower than angle 8 t(28.6) = -4.69, p <0.001. Taken together, the results suggest that in the absent condition, angle has a limited and weak effect whereas in the present condition, angle has a stronger and more widespread effect.
summary_data %>%
ggplot(aes(x = condition, y = mean, group = angle, color = angle)) +
geom_line() +
geom_point() +
geom_errorbar(aes(ymin = mean - se, ymax = mean + se, width = 0.1)) +
scale_color_manual(values = c("#440154FF","#1565c0", "#FF9993")) +
labs(x = "Condition", y = "Latency (ms)", color = "Angle") +
theme_minimal()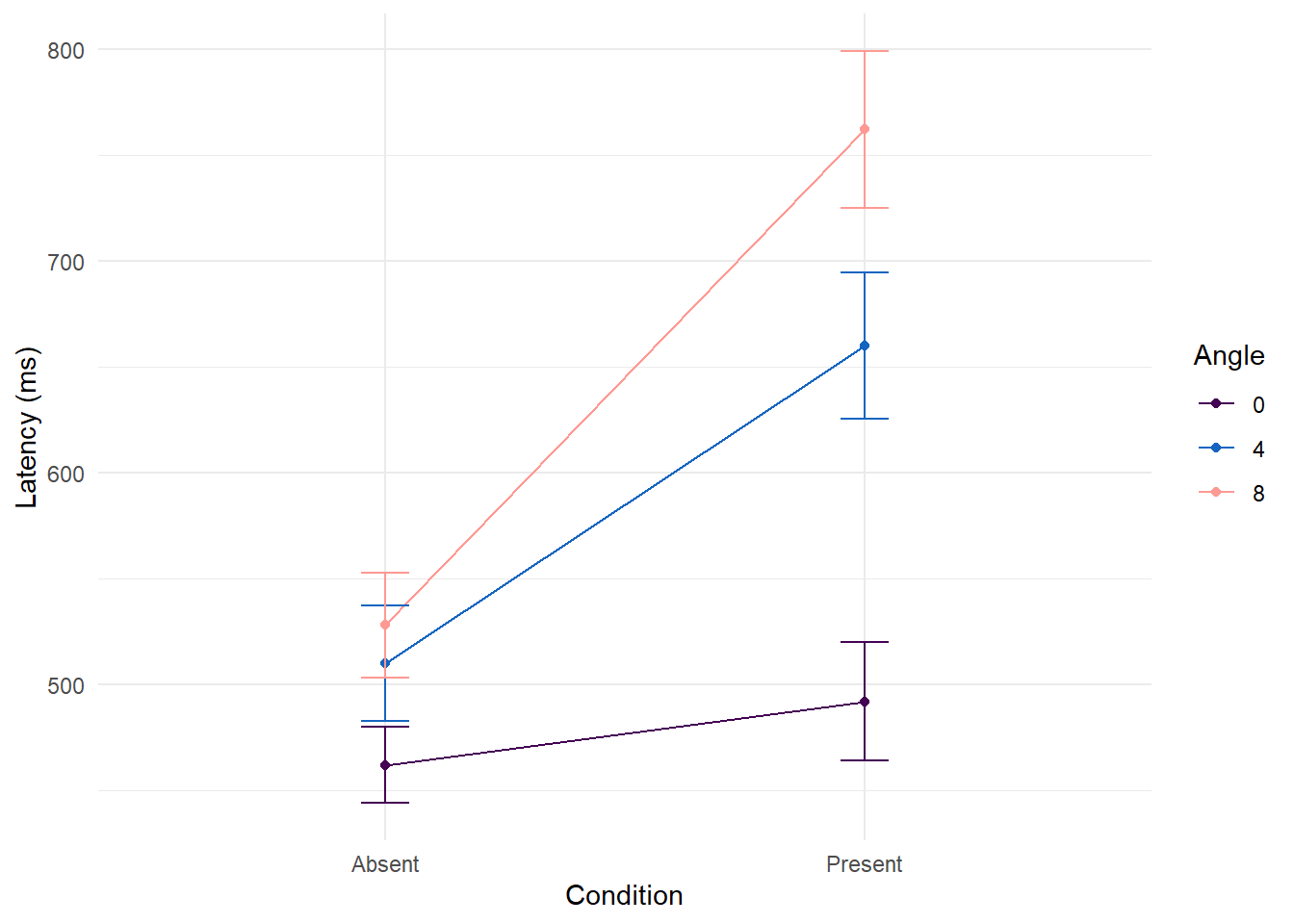
Effect of condition within each level of angle
In the case of condition within each level of angle, we can conduct three separate one-way repeated measures ANOVAs. To control for family wise error rate, a Bonferroni (.05/3, or 0.017) adjustment was implemented. These results reveal significant simple-effects of condition within angle 4 F(1,9) = 19.74, p = 0.002 and condition within angle 8 F(1, 9) = 125.59, p < 0.001. In each of these comparisons mean latencies from the present condition were higher than those in the absent condition. Since condition is only two levels, not further pairwise comparisons are needed.
c("0", "4", "8") %>%
purrr::map_df(
.,
~ summary(aov(latency ~ condition + Error(id/condition),
data = (rm_data %>% filter(angle == .x))))[[2]][[1]] %>%
as.data.frame() %>%
drop_na()
) %>%
mutate(Source = c("Condition w/in 0", "Condition w/in 4", "Condition w/in 8")) %>%
select(Source, everything()) %>%
format_gt_tbl()| Source | Df | Sum Sq | Mean Sq | F value | Pr(>F) |
|---|---|---|---|---|---|
| Condition w/in 0 | 1.000 | 4500 | 4500 | 1.55 | 0.244 |
| Condition w/in 4 | 1.000 | 112500 | 112500 | 19.74 | 0.002 |
| Condition w/in 8 | 1.000 | 273780 | 273780 | 125.59 | < 0.001 |
summary_data %>%
ggplot(aes(x = angle, y = mean, group = condition, color = condition)) +
geom_line() +
geom_point() +
geom_errorbar(aes(ymin = mean - se, ymax = mean + se, width = 0.1)) +
labs(y = "Latency (ms)", x = "Angle", color = "Condition") +
theme_minimal()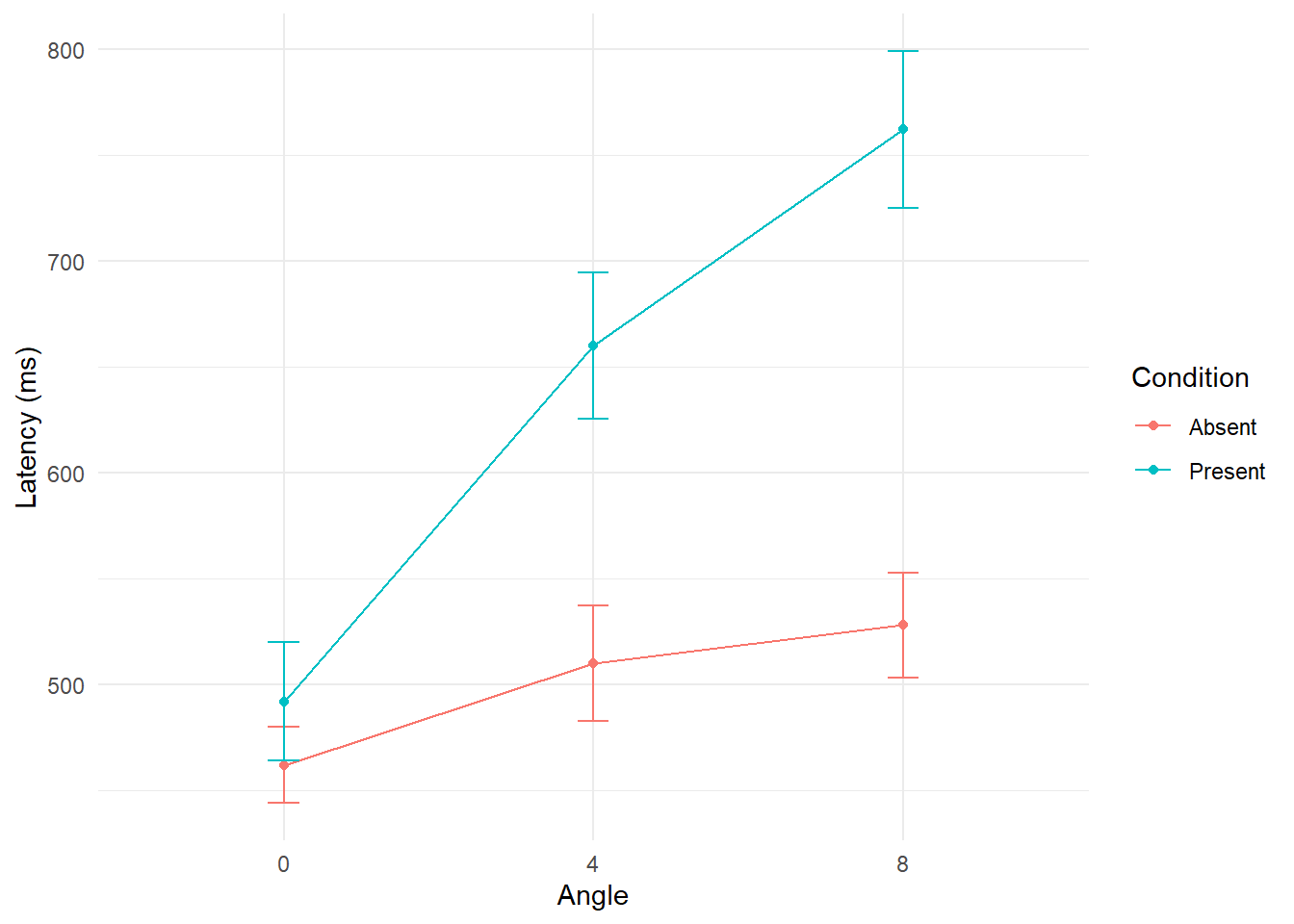
Two-way repeated measures ANOVA with afex package
As noted in the one-way repeated measures ANOVA tutorial, the afex package is helpful to conduct Mauchly’s test for sphericity and to perform adjusted tests. Since there are two within-subjects factors, they can be entered as a character vector in the within = option.
univariate_model2 <- afex::aov_ez(
id = "id",
dv = "latency",
data = rm_data,
within = c("angle", "condition"))summary(univariate_model2)| Source | Sum Sq | num Df | Error SS | den Df | F value | Pr(>F) |
|---|---|---|---|---|---|---|
| (Intercept) | 19425660 | 1 | 292140 | 9 | 598.45 | < 0.001 |
| angle | 289920 | 2 | 64080 | 18 | 40.72 | < 0.001 |
| condition | 285660 | 1 | 76140 | 9 | 33.77 | < 0.001 |
| angle:condition | 105120 | 2 | 20880 | 18 | 45.31 | < 0.001 |
Mauchly’s test for sphericity
As in the tutorial for the one-way repeated measures ANOVA, the afex package can generate the results of Mauchly’s test for sphericity. In the present example data, the condition factor consists of two levels, “Absent” and “Present”. In situations, where the repeated factor has two and only two levels, the assumption of sphericity is automatically satisfied. As a result, the output of summary(univariate_model2) will not display a Mauchly’s test for the condition factor. We will however see the tests for angle and the interaction between angle and condition. Both p-values for these effects indicate a non-signicant finding indicating that the sphericity assumption has not been violated. However as noted before, the results of Mauchly’s test can depend on the distribution of the data and adjusted tests are automatically provided.
# Mauchly's Test for sphericity results
summary(univariate_model2)[[6]][,] %>%
as.data.frame() %>%
mutate(Source = rownames(.)) %>%
select(Source, everything()) %>%
format_gt_tbl()| Source | Test statistic | p-value |
|---|---|---|
| angle | 0.960 | 0.850 |
| angle:condition | 0.894 | 0.638 |
Adjusted tests
# Adjusted tests
summary(univariate_model2)[[5]] %>%
as.data.frame() %>%
mutate(Source = rownames(.)) %>%
select(Source, everything()) %>%
format_gt_tbl()| Source | GG eps | Pr(>F[GG]) | HF eps | Pr(>F[HF]) |
|---|---|---|---|---|
| angle | 0.962 | < 0.001 | 1.22 | < 0.001 |
| angle:condition | 0.904 | < 0.001 | 1.12 | < 0.001 |
References
Maxwell, Scott, Harold Delaney, and Ken Kelley. 2020. AMCP: A Model Comparison Perspective. https://CRAN.R-project.org/package=AMCP.
Maxwell, Scott E, Harold D Delaney, and Ken Kelley. 2017. Designing Experiments and Analyzing Data: A Model Comparison Perspective. Routledge.
Wickham, Hadley. 2019. Tidyverse: Easily Install and Load the ’Tidyverse’. https://CRAN.R-project.org/package=tidyverse.