One-way repeated measures ANOVA

library(tidyverse)
library(AMCP)

A repeated measures ANOVA is an analysis approach that can be used on data gathered from experimental designs where observations from the same unit(participant, animal) are captured multiple times. This within-subject design can be advantageous because each subject can serve as their own control and it can increase power because variability due to individual differences is reduced.

Data set description

In a hypothetical study, the age-normed general cognitive scores form the McCarthy Scales of Children’s Abilities (MSCA) of 12 children were collected at 4 different time points (30, 36, 42, and 48 months of age). These data are presented in Table 5 of Chapter 11 of AMCP package. A repeated measures ANOVA is one approach to analyze these data to adress the research question of whether the mean MSCA scores differ across time points.

# Load the data
data("chapter_11_table_5")

# Set to objected named data
data <- chapter_11_table_5

# Display as table
data %>%
  format_gt_tbl()

Months30	Months36	Months42	Months48
108	96	110	122
103	117	127	133
96	107	106	107
84	85	92	99
118	125	125	116
110	107	96	91
129	128	123	128
90	84	101	113
84	104	100	88
96	100	103	105
105	114	105	112
113	117	132	130

Prepare the data (wide to long)

Before proceeding, we will create a column containing the subject ID number. Since these identifiers are not numeric quantities, we will convert the to factor or character format. Next, we reshapt the data set to long format using the pivot_longer() function. This transformation will facilitate analyses, plotting, and summarizing data.

rm_data <- data %>%
  mutate(id = as.character(seq(1:dim(data)[1]))) %>%
  group_by(id) %>%
  pivot_longer(cols = Months30:Months48, values_to = "score",  names_to  = "age") %>%
  ungroup()

Here’s a view of the first several rows of the long format data. In this format, each subject should have 4 rows of data, one for each timepoint. Since there are 12 subjects total, the entire data sate in this form will be 48 rows long.

rm_data %>%
  head() %>%
  format_gt_tbl()

id	age	score
1	Months30	108
1	Months36	96
1	Months42	110
1	Months48	122
2	Months30	103
2	Months36	117

Generate summary statistics

Next we generate some summary statistics to inspect the data after grouping by age.

rm_data %>% 
  group_by(age) %>%
  summarise(
    n = n(),
    min = min(score),
    max = max(score),
    median = median(score),
    mean = mean(score),
    sd = sd(score)   
    ) %>%
  format_gt_tbl()

age	n	min	max	median	mean	sd
Months30	12	84	129	104.00	103	13.71
Months36	12	84	128	107.00	107	14.16
Months42	12	92	132	105.50	110	13.34
Months48	12	88	133	112.50	112	14.76

Plot the data

One option is to plot the quartiles and means with boxplots to gain a visual sense of the distribution of scores.

rm_data %>%
  ggplot(aes(x = age, y = score, color = age, fill = age)) +
  geom_boxplot(alpha = 0.5) +
  stat_summary(fun = mean, geom = "point", shape = 5, size = 3, stroke = 1) +
  theme_minimal() + 
  theme(legend.position = "none")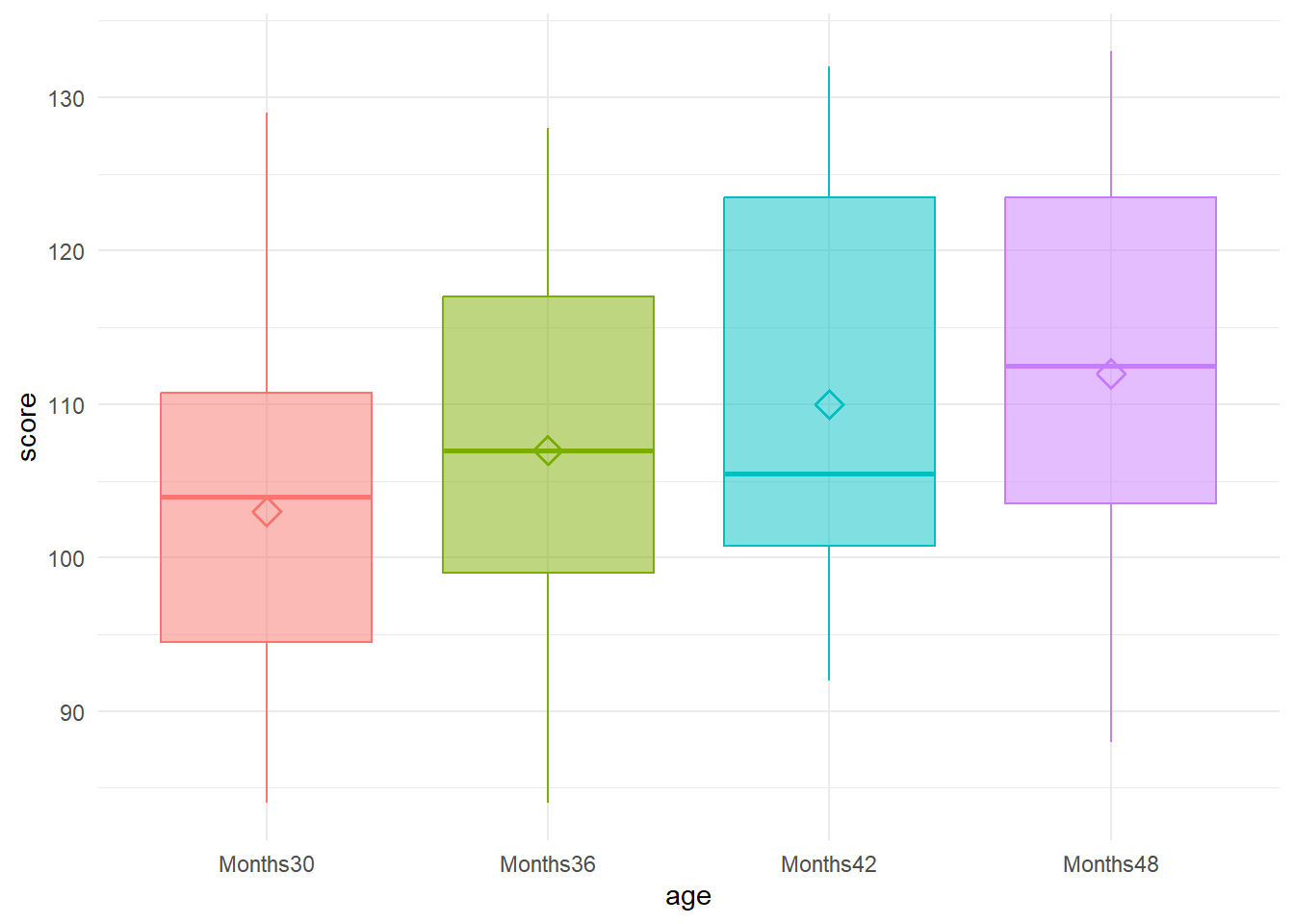

Univariate one-way repeated measures ANOVA

There are two general approaches to analyzing data from a repeated measures design within the ANOVA framework. The following section outlines the univariate approach, while the multivariate approach will be discussed later. Within the univariate framework, there are multiple ways to implement the analysis in R. We begin by using the base R aov() function to specify a model in which MSCA scores are predicted by age, with an error term included to account for the repeated measures structure. The error term Error(id/age) indicates that age is nested within each subject ID, reflecting that repeated observations are taken from the same individuals over time. After fitting the model, the summary() function can be used to display the results.

univariate_model <- aov(score ~ age + Error(id/age), data = rm_data)

summary(univariate_model)

Source	Df	Sum Sq	Mean Sq	F value	Pr(>F)
age	3	552	184.00	3.03	0.043
Residuals	33	2006	60.79	NA	NA

In this approach we observe a significant effect of age, indicating that the means at each time point are not equal. However, a major drawback of using the univariate approach with the base R aov() function is that it does not produce any adjusted tests for violations of sphericity. One key assumption for the univariate approach is sphericity, which is analagous to the homogeneity of variance assumption in a between-subjects design. However, instead of applying to the observed scores, sphericity pertains to the variances of the pairwise difference scores between repeated measures. In other words, sphericity assumes that the variance of all unique pairwise differences is equal across conditions (time in this case).

When the assumption of sphericity is violated, adjusted tests are preferred to protect against inflated Type I error rates. To generate these adjusted tests in R, a package beyond base functionality is required. The afex package is one such tool that can produce adjusted tests in a one-way repeated measures design, including corrections like Greenhouse-Geisser and Huynh-Feldt. In addition, the afex package can output the results of Mauchly’s test for sphericity.

univariate_model2 <- afex::aov_ez(
  id = "id", 
  dv = "score", 
  data = rm_data, 
  within = "age")

summary(univariate_model2)

Source	Sum Sq	num Df	Error SS	den Df	F value	Pr(>F)
(Intercept)	559872	1	6624	11	929.74	< 0.001
age	552	3	2006	33	3.03	0.043

Mauchly’s test for sphericity

A statistically significant result from Mauchly’s test indicates a violation of the sphericity assumption. In such cases, it is preferable to report adjusted test results to reduce the risk of committing a Type I error.

However, Mauchly’s test is not without its criticisms. Its performance can be influenced by the distribution of the data. It can be overly conservative in heavy-tailed distributions and overly liberal in short-tailed ones. These issues are often amplified in larger sample sizes, while in smaller samples the test may lack sufficient power to detect violations. Therefore, it is important to interpret the results of Mauchly’s test with caution and consider alternative analytical approaches that do not rely on the assumption of homogeneity of treatment differences, such as the multivariate approach described later.

summary(univariate_model2)[[6]][,]  %>%
  as.data.frame() %>%
  rename(age = ".") %>%
  mutate(Source = rownames(.)) %>%
  pivot_wider(values_from = "age", names_from = "Source") %>%
  mutate(Source = "age") %>%
  select(Source, everything()) %>%
  format_gt_tbl()

Source	Test statistic	p-value
age	0.243	0.018

Adjusted tests

Adjusted tests can be accessed by indexing the fifth element of the univariate_model2 object. GG eps refers to Greenhouse-Geisser’s epsilon, a correction method that adjusts the degrees of freedom in the F-ratio to account for violations of the sphericity assumption. This value, often denoted as “epsilon hat,” ranges from 0 to 1, with lower values indicating more severe violations of sphericity. The Pr(>F[GG]) value represents the p-value of the F-test using the adjusted degrees of freedom. In this case, we fail to reject the null hypothesis and conclude that the mean MSCA scores across ages are statistically equivalent.

HF eps refers to the Huynh-Feldt epsilon, often called “epsilon tilde,” and is another method for adjusting degrees of freedom in repeated measures ANOVA. It is derived from the Greenhouse-Geisser epsilon and can be viewed as a refinement of “epsilon hat.” When epsilon hat exceeds 0.75, many statisticians recommend using the Huynh-Feldt correction instead, as the Greenhouse-Geisser adjustment may be overly conservative in such cases. In this analysis, the conclusion remains consistent with the Greenhouse-Geisser adjusted test: there is no statistically significant difference between the mean scores across age time points.

Source	GG eps	Pr(>F[GG])	HF eps	Pr(>F[HF])
age	0.610	0.075	0.725	0.064

Pairwise comparisons and confidence intervals

One of the advantages of using the afex package is its seamless integration with the emmeans package for conducting pairwise comparisons. In this dataset, the adjusted tests were not statistically significant, so follow-up pairwise comparisons would typically not be warranted. The following code is provided purely for illustrative purposes.

When displaying t-values from pairwise comparisons, it is important to consider the associated degrees of freedom. In the table below, the degrees of freedom are calculated as N − 1, which suggests that a contrast-specific error term was used in computing the t-statistics. An adjustment for multiple comparisons can also be implemented in the adjust = option.

em <- emmeans::emmeans(univariate_model2, ~ age)

# Produces the same results that would be obtained in SAS
cbind(
  # t values for pairswise comparisons
  (pairs(em, adjust = "none") %>%
    as.data.frame()),
  
  # confidence intervals
  (confint(pairs(em, adjust = "none"), level = 0.95) %>%
  as.data.frame() %>%
  select(lower.CL, upper.CL))
) %>%
  format_gt_tbl()

contrast	estimate	SE	df	t.ratio	p.value	lower.CL	upper.CL
Months30 - Months36	-4	2.58	11	−1.55	0.149	−9.68	1.68
Months30 - Months42	-7	3.05	11	−2.30	0.042	−13.70	−0.30
Months30 - Months48	-9	3.69	11	−2.44	0.033	−17.13	−0.87
Months36 - Months42	-3	2.76	11	−1.09	0.300	−9.07	3.07
Months36 - Months48	-5	4.32	11	−1.16	0.271	−14.50	4.50
Months42 - Months48	-2	2.23	11	−0.90	0.390	−6.91	2.91

Interpretation

Mauchly’s Test of Sphericity indicated that the assumption of sphericity was violated, χ²(4) = 0.24, p = 0.018; therefore, degrees of freedom were corrected using the Greenhouse-Geisser estimate of sphericity. A one-way repeated measures ANOVA, adjusted using the Greenhouse-Geisser correction, revealed no significant effect of Age on McCarthy Scales of Children’s Abilities (MSCA) scores, F(3, 33) = 3.03, p = .075.

Multivariate one-way repeated measures ANOVA

There are a few different ways that one could perform a multivariate ANOVA on these repeated measures. The one illustrated here involves creating a set of difference scores or D variables. With 4 time points, one needs 3 different D variables. In this example the D variables are created as the differences between Months36 and Months 30, Months42 and Months36, and Months48 and Months42. The D variables are then used as the outcomes in the manova() function.

# Version 2 of the multivariate approach using manova()
data <- data %>%
  mutate(D1 = Months36 - Months30,
         D2 = Months42 - Months36,
         D3 = Months48 - Months42)

multivariate_model2 <- manova(cbind(D1, D2, D3) ~ 1, data = data)

Once the model is fitted, we can extract the multiple types of F-test which in this case all result in the same omnibus F-value of 2.24 and the p-value of 0.15.

# MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no age Effect.
c("Pillai", "Wilks", "Hotelling-Lawley", "Roy") %>%
  purrr::map_df(
    ~ anova(multivariate_model2, test = .x) %>%
      as.data.frame() %>%
      drop_na() %>%
      mutate(Statistic = .x) %>%
      rename(Value = sym(.x)) %>%
      select(Statistic, everything())
    )  %>%
  format_gt_tbl()

Statistic	Df	Value	approx F	num Df	den Df	Pr(>F)
Pillai	1.000	0.427	2.24	3	9	0.153
Wilks	1.000	0.573	2.24	3	9	0.153
Hotelling-Lawley	1.000	0.747	2.24	3	9	0.153
Roy	1.000	0.747	2.24	3	9	0.153

In this case, the omnibus test is not significant and there are no post-hoc comparisons to further explore. However, had we observed a significant omnibus test, one approach would be perform the pairwise comparisons would be to conduct a one-sample t-test on the D variables and calculate the standard error manually.

# One-sample t-test on the difference scores
c("D1", "D2", "D3") %>%
  purrr::map_df(
    ~ data %>%
      pull(.x) %>%
      t.test() %>%
      broom::tidy() %>%
      mutate(variable = .x,
             se = estimate/statistic) %>%
      select(variable, estimate, se, p.value, parameter, conf.low, conf.high)
  ) %>%
  format_gt_tbl()

variable	estimate	se	p.value	parameter	conf.low	conf.high
D1	4	2.58	0.149	11	−1.68	9.68
D2	3	2.76	0.300	11	−3.07	9.07
D3	2	2.23	0.390	11	−2.91	6.91

Summary

In this guide, two different approaches were to analyzing data from a one-way within subjects design. For the example data set used, we first analyzed the data with the univariate approach. However, one of the assumptions of the univariate approach, sphericity, was not met and we thus used an adjusted test. In practice, the sphericity assumption is rarely met. As a result, we turned to the multivariate approach using a set of D variables that we created. While these two approaches are valid ways of analyzing these data, they have limitations in the sense that they cannot accomodate missing values. In addition, the multivariate approach has limitations in it’s ability to accomodate covariates that could be of interest. To overcome these limitations, it may preferable to analyze these data using a linear mixed effect model framework which is covered in a separate guide.

References

Maxwell, Scott, Harold Delaney, and Ken Kelley. 2020. AMCP: A Model Comparison Perspective. https://CRAN.R-project.org/package=AMCP.

Maxwell, Scott E, Harold D Delaney, and Ken Kelley. 2017. Designing Experiments and Analyzing Data: A Model Comparison Perspective. Routledge.

Wickham, Hadley. 2019. Tidyverse: Easily Install and Load the ’Tidyverse’. https://CRAN.R-project.org/package=tidyverse.