One-way ANOVA

The one-way ANOVA is a commonly used statistical technique to compare the means of a continuous variable among two or more groups (categorical variable). This guide covers how to perform a one-way between-subjects ANOVA in R. The primary assumptions of ANOVA are independence between groups, normally distributed residuals, and homogeneity of variance. When the homogeneity of variance assumption is violated, consider a Welch’s ANOVA.

The data set

This guide relies on toy data from Exercise 9 in Chapter 3 of the AMCP package. In this exercise, a psychologist randomly assigned 12 subjects to one of 4 different therapy treatments. These treatments consisted of rational-emotive, psychoanalytic, client-centered, and behavioral therapies coded as 1 through 4 respectively. The 4 different treatments were used to investigate which therapy is more effective at reducing phobia scores.

For these data, Group represents the type of therapy the participant was assigned to. Scores represent the score from a post-therapy fear scale where higher numbers indicate higher levels of phobia. Finally, each row represents the group and scores for one subject.

Group	Scores
1	2
1	4
1	6
2	10
2	12
2	14
3	4
3	6
3	8
4	8
4	10
4	12

Perform ANOVA tests

Jmv is an R package that comes from the standalone [jamovi](https://jamovi.org/) statistical spreadsheet software. Jamovi was designed as an alternative to costly statistical analysis software packages like SPSS or SAS and runs R underneath the hood.

With the ANOVA() function, we will predict Scores by Group (Scores ~ Group), set the data to be analyzed as C3E9 and ss = "3" to use the Type III sums of squares. The effectSize = 'partEta' will output the partial eta squared effect size for the omnibus test. We will also set the postHocCorr = 'bonf' to conduct Bonferroni corrected post hoc tests (although tukey can be used as well), postHocES = "d" will compute Cohen’s d effect sizes for the post hoc tests. Lastly, we want to set emmMeans = ~ Group and emmPlots = TRUE to plot estimated marginal means and confidence intervals.

library(jmv)
library(AMCP)

data(C3E9)

# Conduct One-way ANOVA test
ANOVA(formula = Scores ~ Group, 
      data = C3E9,
      ss = "3",
      effectSize = 'partEta',
      postHoc = ~ Group,
      postHocCorr = 'bonf',
      postHocES = "d",
      emMeans = ~ Group,
      emmPlots = TRUE,
      ciWidthEmm = 95)

## 
##  ANOVA
## 
##  ANOVA - Scores                                                                             
##  ────────────────────────────────────────────────────────────────────────────────────────── 
##                 Sum of Squares    df    Mean Square    F           p            η²p         
##  ────────────────────────────────────────────────────────────────────────────────────────── 
##    Group             120.00000     3      40.000000    10.00000    0.0044074    0.7894737   
##    Residuals          32.00000     8       4.000000                                         
##  ────────────────────────────────────────────────────────────────────────────────────────── 
## 
## 
##  POST HOC TESTS
## 
##  Post Hoc Comparisons - Group                                                                                 
##  ──────────────────────────────────────────────────────────────────────────────────────────────────────────── 
##    Group         Group    Mean Difference    SE          df          t            p-bonferroni    Cohen's d   
##  ──────────────────────────────────────────────────────────────────────────────────────────────────────────── 
##    1        -    2              -8.000000    1.632993    8.000000    -4.898979       0.0071719    -4.000000   
##             -    3              -2.000000    1.632993    8.000000    -1.224745       1.0000000    -1.000000   
##             -    4              -6.000000    1.632993    8.000000    -3.674235       0.0376264    -3.000000   
##    2        -    3               6.000000    1.632993    8.000000     3.674235       0.0376264     3.000000   
##             -    4               2.000000    1.632993    8.000000     1.224745       1.0000000     1.000000   
##    3        -    4              -4.000000    1.632993    8.000000    -2.449490       0.2398111    -2.000000   
##  ──────────────────────────────────────────────────────────────────────────────────────────────────────────── 
##    Note. Comparisons are based on estimated marginal means

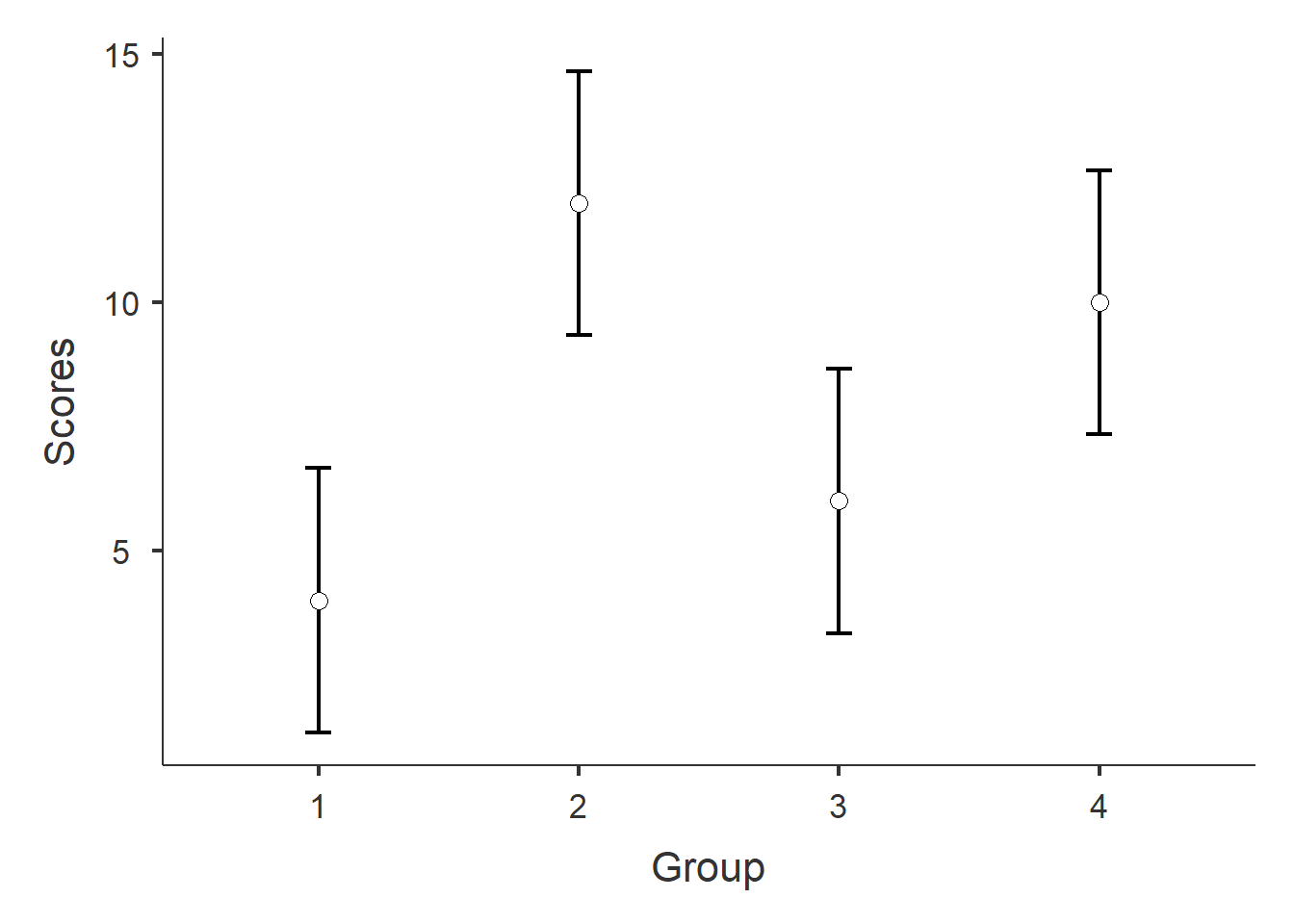
Figure 1: Plot of mean Scores and 95% confidence intervals by group.

Nota Bene

When using the postHocES = "d" option, it may be necessary to update the jmv package remotely. This will depend on the version of jmv installed from CRAN. One way to get the latest updates for jmv is to run the following commands and then restarting RStudio. I’ve noticed that without the updates the Cohen’s d effect sizes can be off, so you may want to double check effect sizes. Finally, you may want to update to the latest R version as some folks have reported R crashing when using the jmv package with some versions of R.

remotes::install_github('jamovi/jmvcore')
remotes::install_github('jamovi/jmv')

Rstatix is another package for conducting statistical tests in R. One of the benefits of the rstatix package is that it works well with the pipe (%>%) operator from the tidyverse/magrittr packages which can facilitate subsetting your data. More importantly, rstatix simplifies much of the manual writing of code for certain statistical test such as the ANOVA. The developer of the rstatix package also maintains the ggpubr package which simplifies producing plots in R. In this guide, I will demonstrate how to conduct a one-way between-subjects ANOVA with rstatix and generate a plot of means with error bars with ggpubr.

library(rstatix)
library(ggpubr)
library(AMCP)
library(tidyverse)

# Load the data
data(C3E9)
data <- C3E9

For this approach, we will need to change our Group variable to factor to specify that our Group variable, although coded as the integers 1 through 4, represent a categorical variable and not a numeric one. Use the str() function on a dataframe or the class() function on a column to determine if your data are factored or not. Then, use the as.factor() function to change Group’s data type.

# Display structure of data (output not shown)
str(C3E9)

# Convert group to factor
C3E9$Group <- as.factor(C3E9$Group)

Next, we use the anova_test() function to conduct the ANOVA. First, specify a formula predicting Scores by Group (Scores ~ Group). Next, specify the dataframe to analyze. Finally, set the effect size output and the sum of squares method to type III. Most commercial statistical software packages and jmv default to the Type III sums of squares and are set as such to mirror the results in the jmv package.

# Conduct ANOVA test
anova_test(Scores ~ Group, 
           data = C3E9, 
           effect.size = "pes", 
           type = 3)

## ANOVA Table (type III tests)
## 
##   Effect DFn DFd  F     p p<.05   pes
## 1  Group   3   8 10 0.004     * 0.789

Post hoc tests

To get the output for the post-hoc tests, we will run the tukey_hsd() function on the same data with the same formula (Scores ~ Group). We can also conduct pair wise comparisons with the pairwise_t_test() function and apply the Bonferroni, Holm, or False Discovery Rate (FDR) correction procedures. In addition, rstatix provides some convenient ways for producing effect sizes and summary statistics.

Tukey’s Honest Significant Difference (HSD)

C3E9 %>%
  tukey_hsd(Scores ~ Group) %>% 
  kable(., "html")

term	group1	group2	estimate	conf.low	conf.high	p.adj	p.adj.signif
Group	1	2	8	2.7705811	13.2294189	0.00523	**
Group	1	3	2	-3.2294189	7.2294189	0.63000	ns
Group	1	4	6	0.7705811	11.2294189	0.02590	*
Group	2	3	-6	-11.2294189	-0.7705811	0.02590	*
Group	2	4	-2	-7.2294189	3.2294189	0.63000	ns
Group	3	4	4	-1.2294189	9.2294189	0.14400	ns

Bonferroni Corrected Tests

# Bonferroni corrected post hoc tests
C3E9 %>% 
  pairwise_t_test(Scores ~ Group, 
                  p.adjust.method = "bonferroni") %>%
  kable(., "html")

.y.	group1	group2	n1	n2	p	p.signif	p.adj	p.adj.signif
Scores	1	2	3	3	0.00120	**	0.00717	**
Scores	1	3	3	3	0.25600	ns	1.00000	ns
Scores	2	3	3	3	0.00627	**	0.03760	*
Scores	1	4	3	3	0.00627	**	0.03760	*
Scores	2	4	3	3	0.25600	ns	1.00000	ns
Scores	3	4	3	3	0.04000	*	0.24000	ns

Effect Sizes

# Effect sizes
C3E9 %>% 
  cohens_d(Scores ~ Group) %>%
  kable(., "html")

.y.	group1	group2	effsize	n1	n2	magnitude
Scores	1	2	-4	3	3	large
Scores	1	3	-1	3	3	large
Scores	1	4	-3	3	3	large
Scores	2	3	3	3	3	large
Scores	2	4	1	3	3	large
Scores	3	4	-2	3	3	large

Summary Statistics

# Summary statistics
C3E9 %>% 
  group_by(Group) %>%
  get_summary_stats() %>%
  kable(., "html")

Group	variable	n	min	max	median	q1	q3	iqr	mad	mean	sd	se	ci
1	Scores	3	2	6	4	3	5	2	2.965	4	2	1.155	4.968
2	Scores	3	10	14	12	11	13	2	2.965	12	2	1.155	4.968
3	Scores	3	4	8	6	5	7	2	2.965	6	2	1.155	4.968
4	Scores	3	8	12	10	9	11	2	2.965	10	2	1.155	4.968

Plot the data

The ggpubr package is a wrapper for ggplot2 and can simplify some of the ggplot2 syntax. In this next code chunk, I use the ggpubr() function on our C3E9 data, specify the x and y variables, set add to "mean" to plot the means, set desc_stat = "mean_ci" to plot the confidence intervals, set error.plot = "errorbar" to draw the error bars, and width = .1 to specify the length of errorbar tips. The rest of the options are straightforward.

ggerrorplot(C3E9,
       x = "Group",
       y = "Scores",
       add = "mean",
       desc_stat = "mean_ci",
       error.plot = "errorbar",
       width = .1,
       color = azl,
       title = "Mean (95% CI)")

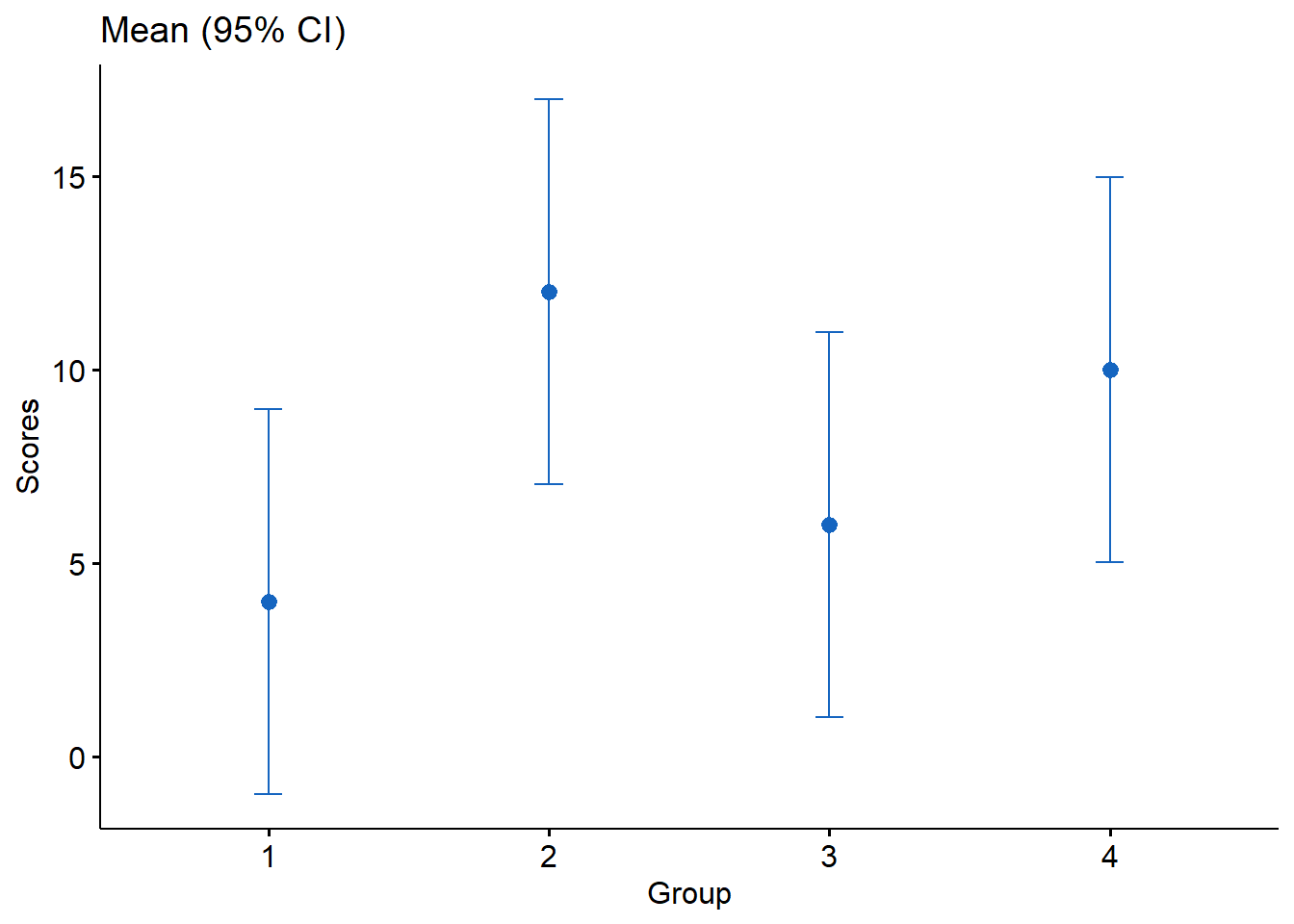
Figure 2: Plot of means and 95% confidence intervals produced by ggpbur.

Back to tabs

Interpret the output

For the omnibus test, we obtained a significant effect of Group [F(3,8) = 10, p < 0.05] which suggests that the means of the 4 groups are not equal. In other words, at least one of the treatments is significantly different than another. To determine where, if any differences between two groups exist, we conducted post-hoc tests on all possible combinations of pairwise comparisons. These tests revealed a significant difference between groups 1 and 2, between groups 1 and 4, and between groups 2 and 3 when correcting for multiple comparisons via the Bonferroni procedure. The results suggest that phobia scores after rational-emotive therapy (1) were lower compared to psychoanalytic (2) and behavioral therapies (4). The results also suggest that phobia scores were on average lower after client-centered therapy (3) compared to psychoanalytic therapy (2). It these were actual data, we would then perhaps conclude with suggesting that rational-emotive therapy may be an optimal approach for treating phobias and that additional research is needed.

Wrap-up

One of the benefits of jmv’s ANOVA() function lies in eliminating the need to write the R code to produce a plot of means, confidence intervals, and effect sizes. In addition, the rstatix package provides additional and more flexible tools for conducting ANOVAs.

References

Kassambara, Alboukadel. 2020a. Ggpubr: ’Ggplot2’ Based Publication Ready Plots. https://CRAN.R-project.org/package=ggpubr.

———. 2020b. Rstatix: Pipe-Friendly Framework for Basic Statistical Tests. https://CRAN.R-project.org/package=rstatix.

Maxwell, Scott, Harold Delaney, and Ken Kelley. 2020. AMCP: A Model Comparison Perspective. https://CRAN.R-project.org/package=AMCP.

Maxwell, Scott E, Harold D Delaney, and Ken Kelley. 2017. Designing Experiments and Analyzing Data: A Model Comparison Perspective. Routledge.

Selker, Ravi, Jonathon Love, and Damian Dropmann. 2020. Jmv: The ’Jamovi’ Analyses. https://CRAN.R-project.org/package=jmv.

Wickham, Hadley. 2019. Tidyverse: Easily Install and Load the ’Tidyverse’. https://CRAN.R-project.org/package=tidyverse.

Last updated on Oct 8, 2023